信号与系统笔记(随堂版)
本文最后更新于:2 个月前
第一章
1.1绪言
‘系统’:是由相互制约又相互作用的个体所组成的具有一定功能的整体
输入信号/激励:施加于系统的信号,可以用$ e(t) \ f(t)$表示
输出信号/响应:系统产生的信号
系统的功能体现:什么样的信号产生什么样的响应
1.2信号的描述及分类
1.2.1 信号的描述
信号可以用一个变量或者多个变量的函数来表示。
1.自变量:时间、空间、频率或者其他量纲的变量
2.因变量:各种物理量或者数量,其可以代表不同物理形态的数学函数或函数的值
时间特性:以时间$t$为自变量,信号可以代表为$t$的函数,用时间$f(t),y(t)$等表征,信号也可以描绘成随时间变化的波形图.信号在莫一时刻的大小、信号持续时间的长短、信号变化的快慢都可以在波形图上反映出来
非时间特性:类空间特征,例如像素图
频率特征:信号在一定条件下可以分解为不同频率的正弦分量之和,正弦分量的振幅和初相位之间的关系叫做频率特征
1.2.2 信号的分类
信号的分类:
- 根据信号是否确切
$$ 信号=\begin{cases} 随机信号 & 信号不确切 = \begin{cases}连续信号 & 时间自变量连续 \离散信号 & 时间自变量离散\end{cases} \ 确定信号 & 信号确定 \end{cases}$$
确定信号: 信号可以写出一个确定的时间函数表达式,对于每一个时刻$t$都有确定的函数值与其对应
随机信号:不能写出确定的时间表达式,只能用概率统计的方法来描述 , 即只能预测该信号在某一时刻的概率 , 而该时刻信号的值是未知的
随机信号在一定条件下可以近似表示为某种确定信号
- 根据信号的时间自变量是否连续
$信号 = \begin{cases}连续信号 & 时间自变量连续 = \begin{cases} 模拟信号 & 信号(函数值)也连续 \ 非模拟信号 & 信号(函数值)不连续 \end{cases} \离散信号 & 时间自变量离散\end{cases} $
连续信号 : 除有限个间断点以外 , 一个信号在任意时刻均有定义值( 允许函数值跳变 )
离散信号 : 只有在一系列离散的瞬间有确切定义而在其他时刻无定义的信号
取样信号 : 时间离散而函数值连续的 , 其幅值可能有无限多个值,不便编成数字码 .
离散信号和连续信号的转换
采样:连续信号—>离散信号
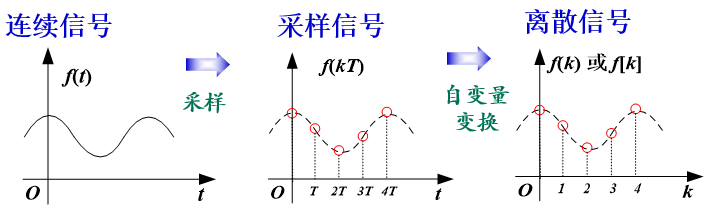
量化:离散信号——>数字信号
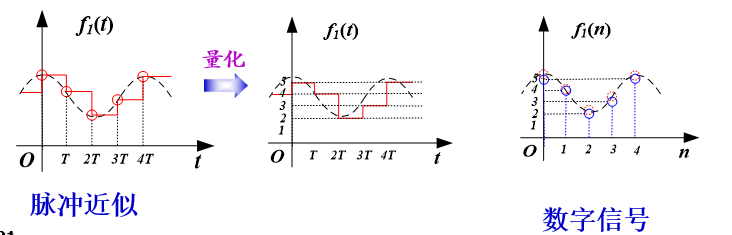
根据信号时间域的定义范围
$信号= \begin{cases}时限信号 &时间域有始有终\有终信号&时间域无始有终\有始信号&时间域有始无终= \begin{cases}因果信号 & 时间是从t=0开始(0,+无穷) \ 反因果信号 & 因果信号的反折(-无穷,0)\end{cases} \ 无时限信号 & 时间域无始无终 \end{cases}$
根据信号的周期性
$信号 = \begin{cases}(连续)周期信号 & 按一定时间周期T周而复始重复出现的&&时间域无始无终的信号\ 非周期信号 & 不具备以上两个条件\end{cases}$
周期信号相加是否为周期信号的判断方法
判断条件:两个信号周期的最小公倍数存在就是周期函数,周期为最小公倍数,否则不存在根据能量是否有界
$信号 = \begin{cases} 能量信号 & 平均功率为0&&总能量为有限制 \ 功率信号 & 平均功率为有限值 &&总能量无限大 \ 非功非能信号 &平均功率无限大&& 总能量无限大\end{cases}$
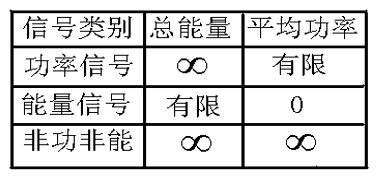
信号 f(t) 能量和功率的计算

根据方程是否是复数
$信号 = \begin{cases}实信号 & 信号方程是实数方程 \ 复信号 & 信号方程是复数方程\end{cases}$
1.3典型信号
1.3.1 典型连续信号
复指数信号
$$f(t)=Ae^{st} = Ae^{\sigma+j\omega t} =Ae^{\sigma}e^{^{j\omega t}}=Ae^{\sigma t}cos\omega t +jAe^{\sigma t}sin\omega t$$
$j\omega t$为复数,称为复频率
$\omega,\sigma$为实数
$\omega=0$为实指数信号
$\sigma=0$为虚指数信号
实指数信号
$f(t)=Ae^σt$

单边衰减指数信号
$$f(t)=\begin{cases}0&t<0\Ae^σt&t≥0)\end{cases}$$
正弦信号
$f(t)=A cos( ωt+ϕ)$
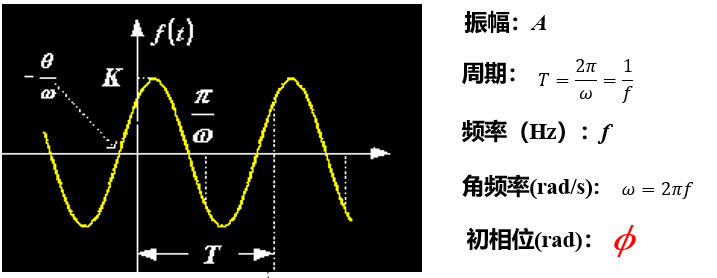
变幅正弦振荡信号
$f(t)=Ae^{σt} cosωt$
$f_r (t)=Re[ Ae^st]=Ae^σt cosω t $
$f_i (t)=Im[ Ae^st]=Ae^σt sinω t $
σ<0:按指数规律衰减的正弦振荡信号;
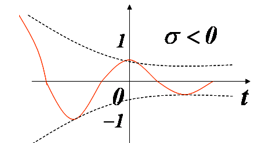
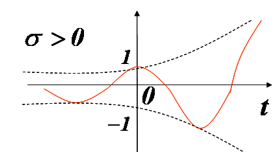
σ>0:按指数规律增长的正弦振荡信号;
抽样信号
$f(t)=Sa(t)= \frac{sin(t)}{t}$
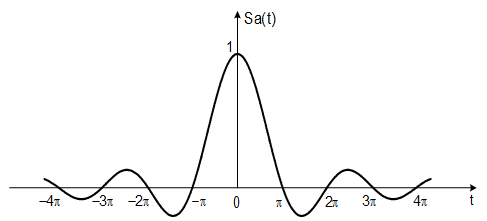
性质:
$$1. Sa(-t)=Sa(t),偶函数
\2. t=0,Sa( t)=1,即即 lim┬(t→0) Sa( t
\3. Sa( t)=0, t=±nπ,n=1,2,3⋯
\4. ∫0^∞〖sint/t dt=π/2, 〗 ∫(-∞)^∞〖sint/t dt=π〗
\5. lim┬(t→±∞)Sa( t)=0
\6. sinc( t)=sinπ t/πt$$高斯脉冲信号(钟形脉冲信号)
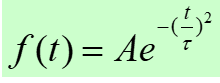
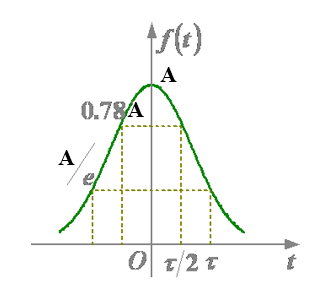
脉冲宽度:当f(t)下降到最大值0.78A时,所对应的两个截止时刻时间的时间范围。常见题型及解题方法
奇异函数
单位斜变信号
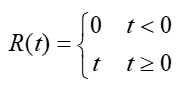
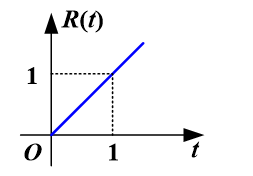
有延迟的单位斜变信号
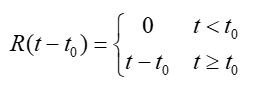
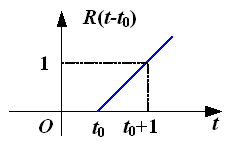
l 截平斜变信号


l 锯齿形脉冲信号


l 正三角脉冲信号


单位阶跃函数(重点)


1.功率信号、能量信号、非功非能信号的判断
判断依据

计算方法

